Мир детерминирован или случаен? Есть ли свобода воли или демон Лапласа возможен? Вопросы не простые, но актуальные на протяжении веков. Пока философы с ними разбираются, попробуем подстелить соломки и научиться считать вероятности и заодно приготовим арбузное мохито.
Классическое определение вероятности
Случайный опыт (эксперимент, наблюдение, испытание) - это некоторое действие, которое можно повторить большое количество раз в одинаковых условиях, а результат этого действия зависит от случая и его невозможно предсказать.
Случайным событием называется событие, которое при осуществлении некоторых условий может произойти или не произойти. Например, выпадение решки при подбрасывании монеты
Случайные события называются несовместными в данном испытании, если никакие два из них не могут появиться вместе. Например, выпадение орла и решки одновременно
Случайные события образуют полную группу, если при каждом испытании может появиться любое из них и не может появиться какое-либо иное событие, несовместное с ними. Например, монета идеальная и не может встать на ребро, полную группу составляют орёл и решка.
Рассмотрим полную группу равновозможных несовместных случайных событий. Такие события будем называть исходами или элементарными событиями. Исход называется благоприятствующим появлению события АА, если появление этого исхода влечет за собой появление события АА.
Вероятностью события A называют отношение числа M благоприятствующих этому событию исходов к общему числу N всех равновозможных несовместных элементарных исходов, образующих полную группу. P(A)=M/N
Свойство 1. Вероятность достоверного события равна 1
Свойство 2. Вероятность невозможного события равна 0.
Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Итак, вероятность любого события удовлетворяет двойному неравенству 0≤P(A)≤1
Попробуем решить достаточно простую задачу на гипергеометрическое распределение. Сложное слово простая суть, это задачи на выбор без возвращения из некоторой совокупности объектов (шаров, деталей, билетов, учебников и т.д.) нужных нам объектов (красных шаров, бракованных деталей, выигрышных билетов и т.д.)
Используем обозначения:
N – общее количество предметов
D – один вид объекта
Вероятность выбрать k определенных объектов из наудачу вынутых без возвращения из n элементов вычисляется по формуле:
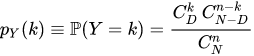
Где биномиальный коэффициент
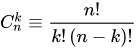
Делаем арбузное мохито:

В большом бокале смешали порванные листья мяты, разрезанный на кусочки лайм и сахар. Толкушкой хорошо раздавили, чтобы лайм пустил сок. Добавили ром и лед. Теперь надо добавить 5 арбузных шариков, все перемешать и выпить отличный коктейль.
Арбузные шарики перемешаны с дынными и находятся в банке с узким горлышком, можно достать только по одному. Мы точно знаем, что в банке есть ровно 6 арбузных и 8 дынных, всего 14. Найдем вероятность, что за 5 доставаний нам удастся сделать арбузное мохито.
Анонимная викторина
Сложная ли задача, пишите в комментариях. Честно считали или интуитивно понятно (плюс/минус), что в результате должно получиться?


Комментарии
50Кстати вот мое мохито с арбузными шариками.
Было вкусно! )
Онлайн калькулятор для расчета факториалов (n!)
Бокальчик прикольный)
Мне тоже нравится ))
Ответочка😉Клубничный)))
Это скорее у меня ответочка на Ваш июнький )
Отличная вещь!
Сезонный мохито😄
Да, это он или оно! У меня путаница с родом
Мохито - напиток. Он мой) Моя логика. Ну сейчас кофе можно начать приплетать, какао))
буррито, мохито, налито - оно. Такая логика ))
с желаниями всё не так! Это совсем не шарики из шляпы.
И законы там совершенно другие. Классический -
Много хочешь - мало получишь.
И вообще.... приходится в таких случаях постоянно оглядываться
Оттого, что мечты у всех разные, нередко происходят трагедии. Одни мечтатели гибнут в результате того, что сбываются мечты других.
Позвольте дать совет: прежде чем мечтать, посмотрите по сторонам. Убедитесь, что поблизости никто не мечтает. А иначе мечты сбудутся, но не уверен, что ваши."
(с)
Это был анекдот ))
Думаете трагедии из-за несовпадения мечт?
конечно! Кто-то же этого желал!
Хм.. ну ладно ))
Трэш) Тыкнул в первый вариант😄
Правильно сделали.
Надо было в четвертый
Не) Верный пишут другой вариант. Ну прикольное задание))) Надо только было разобраться что подставлять вместо N k n D. Что я не сделал😄Но вы все подставляйте, не поступайте как я😄😄😄
Я надеялась, что задачка на интуитивном уровне может решиться, конечно не точно, но хотябы приблизительно порядок величины
Если под рукой есть листок бумаги и карандаш, то я лучше на бумаге порешаю
она и решается интуитивно. речь идет о умножении вероятностей. максимальная вероятность - 6/14, минимальная - 2/10. количество событий 5. из предложенных вариантов самый подходящий - четвертый. немного запутало бы, если вместо вероятности больше 1 указать среднее от суммы пяти вероятностей.-)))
Я не могла обойти стороной значение больше 1 и 0,5 )
больше 1 противоречит вероятности достоверного события.-) 0.5 - ну хорошо, для блондинок.-))))
Конечно ))
как это?? а как же знаменитые 146% или если без процентов, то 1,46 ?
а можно и во второй: как в анекдоте про вероятность встречи с динозавром - то ли встретишь, то ли нет, то есть 50/50 😂
Да, это тест на "блондинку" ))
Этого я и боялась. Формулы это страшно.
Это прекрасно!!! Надо было просто дожимать. Где-то что-то не то подставил.
Я уж подумала, что формулу не правильную выставила. Вот так надо:
Ну вот чутка не попал) Почему 0/8 и 5/14? Вот здесь я поспешил)
У нас 8 дынных шариков и они нам совсем не нужны их должно быть 0, т.е. 0 из 8
Достаем 5 из 14, в знаменателе
Ааа, это типа оставшийся элемент в выборке?
Вот здесь брал все арбузы, а не доставания)) Вчитываться в условию - нееее! Только импровизация, только хардкор😁
У меня такое часто. Потом еще по три раза решаю, чтоб наконец то решить нормально ))
Виктория, классный пост и интересное задание🚀Спасибо😉
Если сказать, что я долго решалась его написать, ничего не сказать
Спасибо за оценку!
А что раздумывали?)
Так же формулы с факториалами. По моему это никто не будет считать, кроме Вас конечно )
Все относительно! Для меня это самый легкий ваш пост😄Есть цифры, формулы. Надо просто не затупить...как я😄
Значит надо было еще подробнее описать. Я с формулами намучилась, их сюда в пост из ворда не вставить. Надо было искать картинку или самой научиться делать картинки из ворда. Это для меня теперь квест. Буду учиться
чё там учиться то? тем более про то что сейчас написано.
Написал что-то в ворде. Сохрани его в нужном формате. ПДФ например, или ПНГ... или... посмотреть надо чё вставляется
Ну вот и вставил
Я попробую. Спасибо!